1.      Introduction

Soit la fonction f(x) = x² + x – 2 sur l’intervalle [-3 ; 2]. Remplir le tableau de valeurs suivant puis tracer la représentation graphique de f(x) sur cet intervalle.

x	-3	-2	-1	-0,5	0	1	2
f(x)	4	0	-2	-2,25	-2	0	4

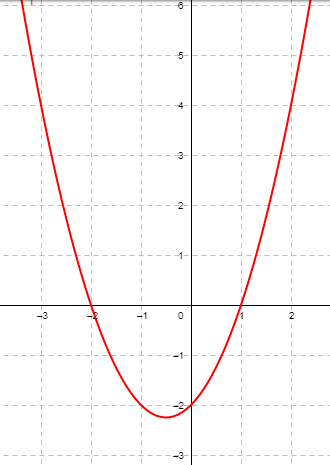
Indiquer les valeurs de x pour lesquelles f(x) = 0.

Pour x = -2 et x = 1.

L’équation du second degré –x² + x – 2 = 0 a donc 2 solutions.

x₁ = -2             x₂ = 1              S = {-2 ;1}

2.      Etude de cas particuliers avec Géogébra.

Cliquer sur le lien pour accéder à Géogébra en ligne : https://www.geogebra.org/m/gBH4Dya4

Résoudre les équations suivantes, puis réécrire l’équation sans parenthèses.

• (x + 1) (x + 2) = 0

x = -1 ou x = -2.          S = {-2 ;-1}

Application calculatrice

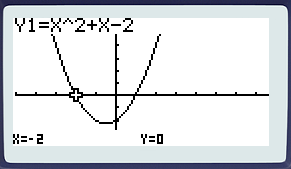
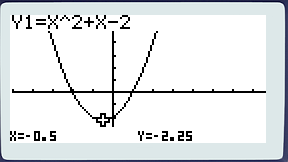
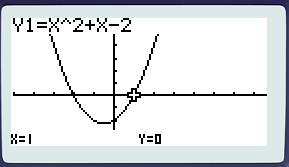
L’équation du second degré x² + 3x + 2 = 0 a donc 2 solutions

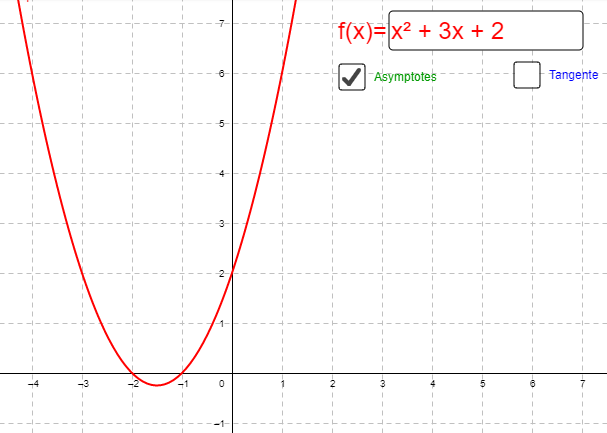
A l’aide du logiciel Géogébra, tracer la fonction

f(x) = x² + 3x + 2.

Que remarque-t-on aux points d’abscisses x = -1 et x = -2 ?

La courbe coupe l’axe des abscisses. f(x) = 0.

• (4x – 2)² = 0

x = 0,5              S = {0,5}

L’équation du second degré 16x² – 16x + 4 = 0 a donc 1 solution unique.

A l’aide du logiciel Géogébra, tracer la fonction

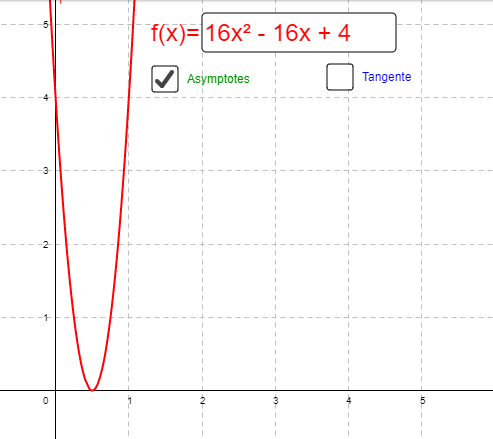
Application calculatrice

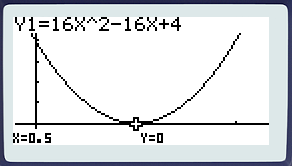
g(x) = 16x² – 16x + 4

Que remarque-t-on aux points d’abscisses x =

La courbe touche l’axe des abscisses. g(x) = 0.

• A l’aide du logiciel Géogébra tracer la fonction h(x) = -2x² + 3x – 5

En déduire graphiquement la résolution de l’équation -2x² + 3x – 5 = 0

Il n’y a pas de solutions car la représentation graphique de h(x) ne coupe pas l’axe des abscisses (il n’existe pas de valeurs de x pour laquelle h(x) = 0). d’où S = {ø}

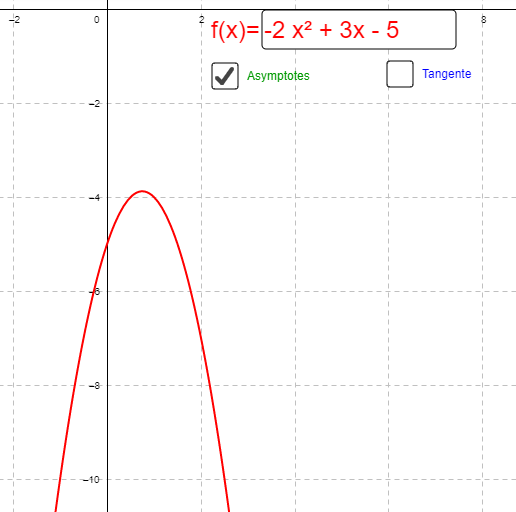
3.      Tableau de variation de fonctions du second degré.

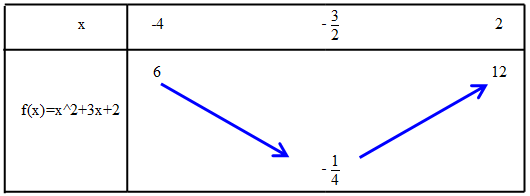
            3.1.      Tableau de variation de la fonction f(x) = x² + 3x + 2 sur l’intervalle [-4 ; 2].

A l’aide de l’étude précédente et du logiciel géogébra, tracer le tableau de variation de la fonction f.

            3.2.      Tableau de variation de la fonction h(x) = -2x² + 3x – 5 sur l’intervalle [-2 ; 4].

A l’aide de l’étude précédente et du logiciel géogébra, tracer le tableau de variation de la fonction h.

3.      Tableau de variation de fonctions du second degré.

            3.1.      Tableau de variation de la fonction f(x) = x² + 3x + 2 sur l’intervalle [-4 ; 2].

A l’aide de l’étude précédente et du logiciel géogébra, tracer le tableau de variation de la fonction f.

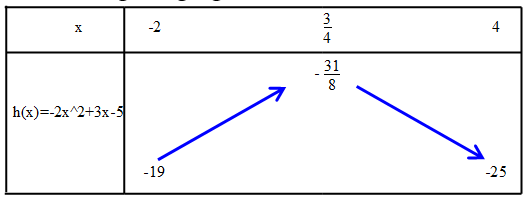
            3.2.      Tableau de variation de la fonction h(x) = -2x² + 3x – 5 sur l’intervalle [-2 ; 4].

A l’aide de l’étude précédente et du logiciel géogébra, tracer le tableau de variation de la fonction h.