Botanique appliquée
Travaux dirigés : Extraits de sujet d’examen
EXERCICE 1
Après avoir mené une enquête auprès de 1 000 personnes, on modélise la progression d’une épidémie de grippe par la fonction définie sur [1 ; 30] par : f(x) = 144 ln(x) + 81 où x représente le nombre de jours et f(x) représente le nombre de personnes contaminées.
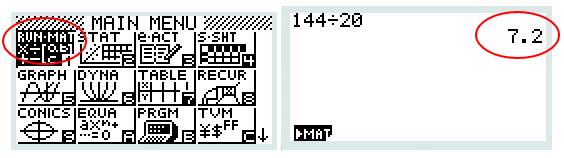
- Déterminer, à l’entier inférieur près, le nombre de contaminés après trois jours d’épidémie.
ELEMENTS DE CORRECTION
2. Déterminer f ’(x).
ELEMENTS DE CORRECTION
Utiliser le formulaire fourni en fin de sujet
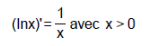
Soit f'(x) = 144 / x
vérification possible
Utiliser une calculatrice en ligne pour dériver la fonction :
https://www.solumaths.com/fr/calculatrice-en-ligne/calculer/deriver
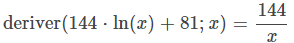
3. Justifier que f ’(x) est positive sur [1 ; 30].
ELEMENTS DE CORRECTION
La variable x appartient à un intervalle positif allant de 1 à 30. Le nombre 144 est également positif. L’ensemble des résultats est donc positif (règle des signes).
4. Déduire du résultat précédant les variations de f.
ELEMENTS DE CORRECTION
Si le signe de la fonction dérivée f’ est positif, alors cela signifie que la fonction f est croissante.
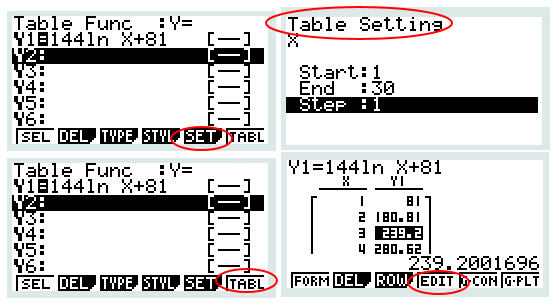
5. Compléter, à l’entier inférieur, le tableau donné ci-dessous :

ELEMENTS DE CORRECTION
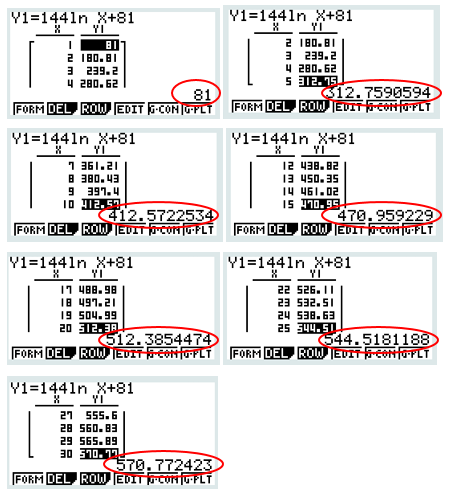
6. Calculer f ’(20).
ELEMENTS DE CORRECTION
7. Déterminer l’équation réduite de la tangente (T) à la courbe représentative de f au point d’abscisse 20. Les coefficients seront donnés à l’unité près.
ELEMENTS DE CORRECTION
Utiliser le formulaire fourni en fin de sujet
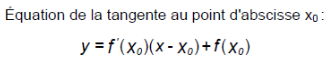

8. On considère la représentation graphique de la fonction f fourni ci-dessous
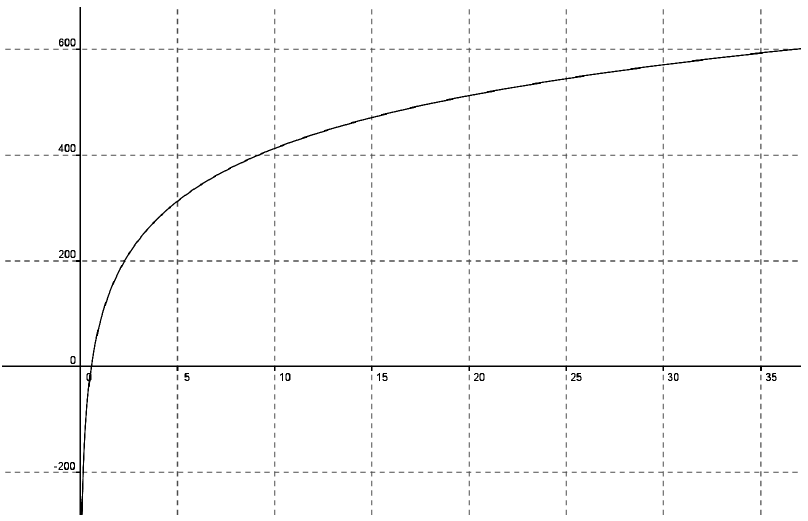
a. Tracer la tangente (T) dans ce repère. (On pourra prendre pour équation de (T) : y = 7x + 370)
b. Par lecture graphique, déterminer au bout de combien de temps 550 personnes seront contaminées ; vous laisserez apparents les traits de construction.
ELEMENTS DE CORRECTION

D’après l’énoncé, x représente le nombre de jours et f(x) représente le nombre de personnes contaminées. La lecture graphique permet de dire que 550 personnes seront contaminées en 26 jours.
c. Il semble que la courbe de f peut être approchée par la tangente (T) autour de 20 jours. Cette proximation est-elle correcte pour trouver au bout de combien de temps 550 personnes seront contaminées ? Peut-on utiliser cette même approximation pour calculer f(50) ? Pourquoi ?
ELEMENTS DE CORRECTION
Le temps nécessaire pour contaminer 550 personnes est de 26 jours. Ce résultat est encore proche de la tangente pour x0=20. L’approximation est encore correct. Toutefois, plus nous nous éloignons de x0=20, plus l’approximation sera inexacte. La courbe représentant la fonction f s’éloigne de la tangente en x0=20. Il sera alors nécessaire de calculer f(50).
9. Le nombre moyen de personnes contaminées par jour se calcule par l’intégrale suivante :
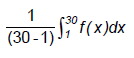
a. Calculer l’intégrale :
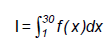
(Le résultat est donné à 10-3 près et le calcul peut être obtenu directement à la calculatrice).
ELEMENTS DE CORRECTION
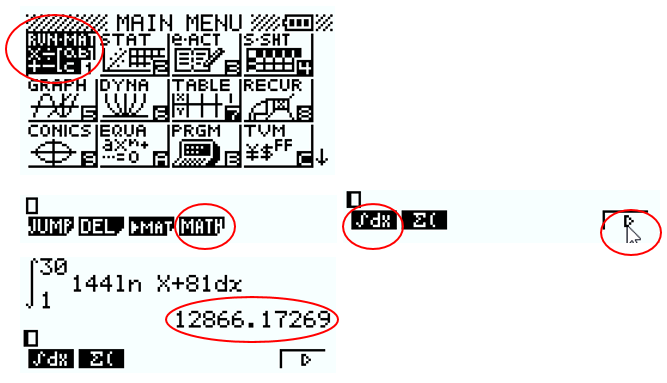
Le résultat du calcul de l’intégrale est donc 12 866,173 à 10-3 près.
b. Montrer que chaque jour, le nombre de contaminés s’élève en moyenne à peu près à 440 personnes. (Le résultat est donné à l’unité).
ELEMENTS DE CORRECTION
A partir du résultat précédant et de la formule proposée dans l’énoncé de la question 9,
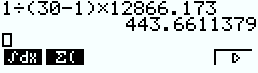
Chaque jours, le nombre de contaminés s’élève en moyenne à 444 personnes.
Formulaire

