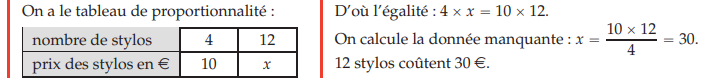Linéarité et proportionnalité

Deux suites de n nombres réels (x₁, x₂, . . . , x_n)et (y₁, y₂, . . . , y_n) sont proportionnelles si tout nombre de l’une est obtenu en multipliant tout nombre de même rang de l’autre par un nombre constant appelé coefficient de proportionnalité, ou par son inverse.
En terme de fonction, l’une est l’image de l’autre par une fonction linéaire f définie par y = f (x) = a . x où le nombre non nul a est le coefficient de proportionnalité.

On reconnaît une situation de proportionnalité lorsque le support des points représentant la situation est une droite passant par l’origine du repère.

Propriété de Linéarité additive

Si deux suites sont proportionnelles, alors f (x₁ + x₂) = f(x₁) + f(x₂), c’est à dire que l’image d’une somme est égale à la somme des images.

Exemple : Si 4 stylos coûtent 10 €, alors 12 stylos = 4 stylos + 4 stylos + 4 stylos coûtent 10 € + 10 € + 10 € = 30 €.

Propriété de Linéarité multiplicative

Soit k un réel non nul, si deux suites sont proportionnelles, alors f(k . x) = k . f(x)

Exemple : Si 4 stylos coûtent 10 €, alors 12 stylos = 3 x 4 stylos coûtent 3 x 10 € = 30 €

Propriété de Coefficient de proportionnalité

Le coefficient de proportionnalité est le coefficient multiplicateur permettant de passer d’une grandeur à une autre (à ne pas confondre avec le coefficient de linéarité multiplicative).

Exemple : Si 4 stylos coûtent 10 €, le coefficient de proportionnalité est de 2,5 car 4 x 2, 5 = 10.
Alors, 12 stylos coûtent 30 € car 12 x 2, 5 = 30.

Propriété de produit en croix

Dans un tableau de proportionnalité, les produits « en diagonale » (ou produits en croix) sont deux à deux égaux. Ceci permet de déterminer une quatrième proportionnelle.

Lorsque l’on veut déterminer une quatrième proportionnelle, on peut résoudre une équation.