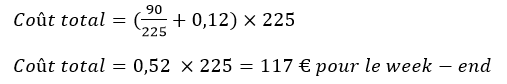Botanique appliquée
Fonction inverse
Etude de la fonction inverse : dérivée, tableau de variations, représentation graphique
Définition
Comme son nom l’indique, la fonction inverse associe à chaque nombre de son ensemble de définition une image qui correspond à l’inverse de ce nombre, elle est définie par la formule:
f(x) = 1 / x
Ensemble de définition
La division est possible par tout nomber réel sauf pour zéro qui est exclu de l’ensemble de définition de la fonction inverse. La fonction inverse est donc définie sur l’inervalle ]- ∞ ; 0[ U ]0 ; + ∞[ que l’on peut également noté R -{0} ou R*
Courbe représentative
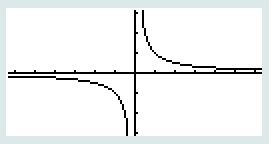
La fonction inverse est représentée par une courbe appelée hyperbole qui est symétrique par rapport à l’origine du repère c’est à dire le point O de coordonées ( 0 ; 0 ). Cette symétrie implique que si un point (x1 ; y1) appartient à la courbe alors le point (-x1 ; -y1) lui appartient aussi. Les variations de la fonction sont plus importantes à proximité de l’origine, par conséquent son tableau de de valeurs doit comporter davantages de points dans cette zone.
Tableau de valeurs
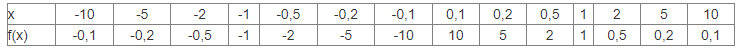
Courbe représentative de la fonction inverse
Saisir la fonction dans le module « graphique » de votre calculatrice

Appuyer sur la touche « F1 » Trace
Fonction dérivée de la fonction inverse
La fonction inverse est dérivable sur chaque intervalle ]-∞; 0[et ]0 ; +∞[. La fonction inverse n’est pas dérivable en 0. La dérivée de la fonction inverse est la fonction f ‘ définie sur ![]() – { 0 } par :
– { 0 } par :

Signe
La fonction inverse est négative sur chaque intervalle ]-∞; 0[et ]0 ; +∞[.
La fonction inverse est strictement décroissante sur chacun des intervalles où elle est définie.
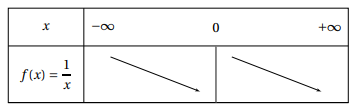
Tableau de Variations
La fonction inverse est décroissante sur l’intervalle ]- ∞ ; 0[ puis sur l’intervalle ]0 ; + ∞[ mais on ne peut pas considérer qu’elle est décroissante sur la totalité de son ensemble de définition en raison de la discontinuité qui existe entre les deux parties de ce dernier.
Exercice 1 : Application en électricité
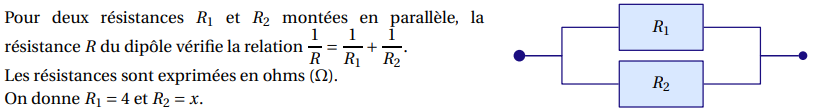

ELEMENTS DE CORRECTION – Exercice 1
Question 1

Question 2
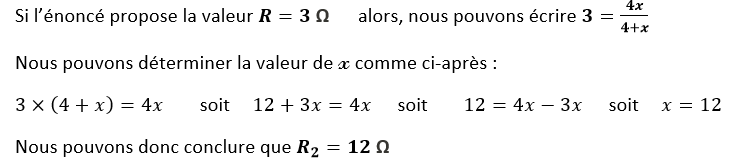
Question 3a
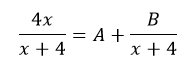
Pour résoudre cette question, il faut décomposer la fraction comme une somme d’un nombre réel entier et d’une fraction strictement inférieure à 1, avec A et B deux nombres réels entiers.
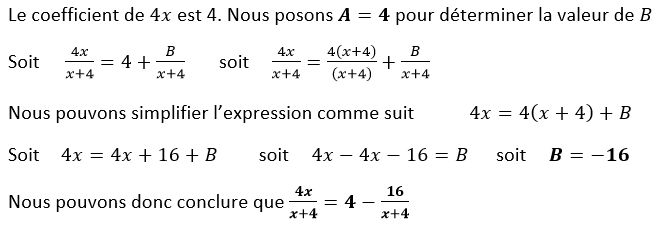
Question 3b
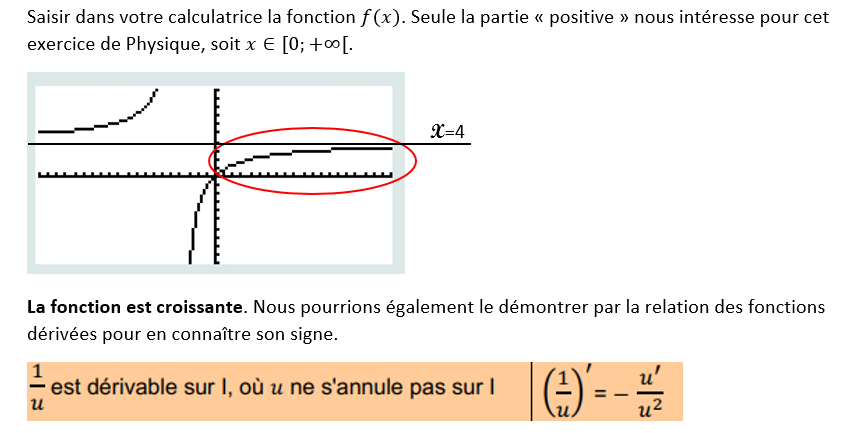
Question 4

Exercice 2 : Coût moyen

EMEMENTS DE CORRECTION – Exercice 2
Question 1
Prix de revient moyen (en €/km parcouru) = Prix location WE (en €/km parcouru) + consommation moyenne (en L/100 km) x prix carburant (€/L)

Question 2a
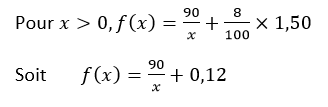
Question 2b

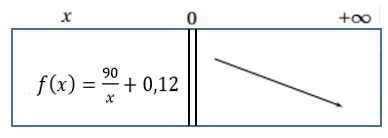

Question 3a
Méthode avec la calculatrice par lecture graphique (touche shift+ F3), paramétrer comme ci-dessous


Pour un prix moyen de 0,52 €/km, nous lisons une distance parcourue proche de 225 km. (résultat approximatif)
Méthode par le calcul (résultat exact)

Question 3b