Mathématiques
Travaux dirigés : Extraits de sujet d’examen
PARTIE A
Un vétérinaire administre un traitement par voie intraveineuse à une brebis. La quantité initiale de médicament dans le sang de la brebis est alors de 18 mg.L-1.
La quantité de médicament, en mg.L-1, qui reste dans le sang de la brebis au bout de x heures est donnée par la fonction f définie sur l’intervalle [0 ; 16] par : f(x) = 18e-0,15x.
1. Calculer f ’(x) pour tout x appartenant à l’intervalle [0 ; 16].
ELEMENTS DE CORRECTION
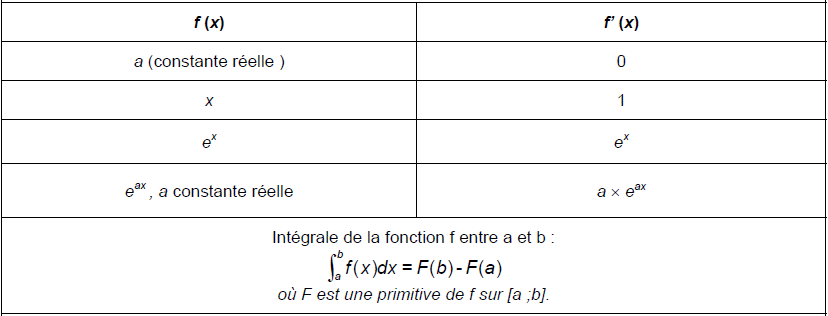
A partir du formulaire situé en fin de sujet, nous pouvons écrire :
f ‘ (x) = 18 . (-0,15) . e-0,15x soit f ‘ (x) = – 2,7 e-0,15x
2. Justifier que f ’(x) est négatif pour tout x appartenant à l’intervalle [0 ; 16]. En déduire les variations de f sur l’intervalle [0 ; 16].
ELEMENTS DE CORRECTION
Pour tout x, l »exponentiel d’un nombre négatif est positif. le coefficient -2,7 étant négatif. Selon la règle des signes, le résultat sera toujours négatif.
Si le signe de la fonction dérivée f ‘ est négatif, alors cela signifie que le sens de variation de la fonction f est décroissante.
3. Compléter le tableau de variations de la fonction donné ci-dessous. On donnera les valeurs exactes ou approchées de f(0) et de f(16).

ELEMENTS DE CORRECTION
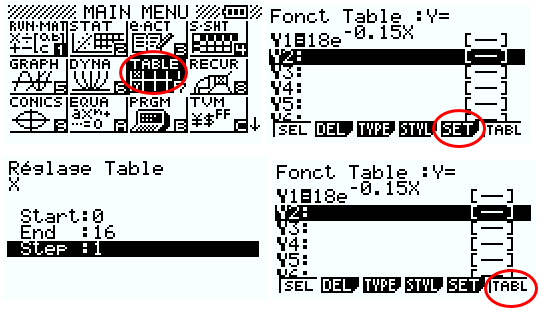
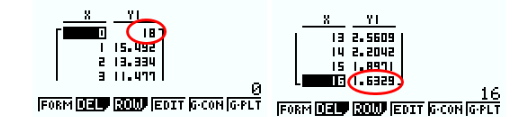

4. Compléter le tableau de valeurs de la fonction f fourni ci-dessous. (les résultats sont arrondis à 10-1 près).

ELEMENTS DE CORRECTION


5. Le traitement cesse de faire effet lorsque la quantité de médicament dans le sang de la brebis est inférieure à 4 mg.L-1. Déterminer au bout de combien d’heures le traitement cesse de faire de l’effet.
ELEMENTS DE CORRECTION
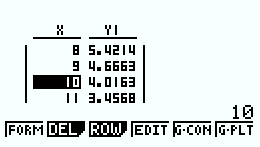
Le traitement cessera de faire effet au bout de 10 heures.
PARTIE B
La quantité moyenne de médicament dans le sang de la brebis par heure lors des 12 premières heures est donnée par la formule suivante :
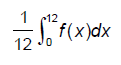
On considère la fonction F définie sur [ 0 ; 16] par : F(x) = -120e-0,15x.
1. Démontrer que F est une primitive de f.
A partir du formulaire situé en fin de sujet, nous pouvons écrire :
F(x) = 18 / (-0,15) e – 0,15 x soit F(x) = -120 e – 0,15 x
2. Calculer
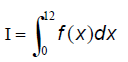
Donner la valeur exacte de I, puis la valeur arrondie à 10-2 près.
ELEMENTS DE CORRECTION
Méthode 1
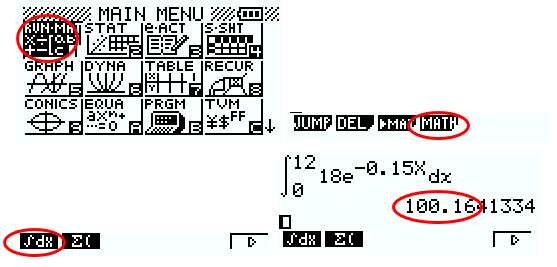
Le résultat de l’intégrale I est 100,16 à 10-2 près.
3. Calculer la quantité moyenne de médicament dans le sang de la brebis par heure lors des 12 premières
heures. Donner la valeur à 10-2 près.
Méthode 2

F(12)-F(0) = 19,9 – 120 = 100,16…
Méthode 3
Utiliser le lien ci-dessous pour calculer en ligne l’intégrale d’une fonction sur un intervalle.
https://www.dcode.fr/integrale-intervalle
ELEMENTS DE CORRECTION
A partir du résultat précédant et de la formule fournie dans l’énoncé, nous pouvons écrire :
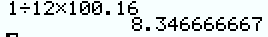
La quantité moyenne de médicament dans le sang de la brebis par heure lors des 12 premières heures est 8,35 mg.L-1
___________________________________________
FORMULAIRE