La règle du produit

Une règle de probabilité très utile en génétique est la règle du produit. Elle énonce que la probabilité de deux (ou plusieurs) événements indépendants survenant ensemble peut être calculée en multipliant les probabilités individuelles des événements. Par exemple, si vous lancez un dé à six faces une fois, vous avez 1/6 chance (1 chance sur 6) d’obtenir un six. Si vous lancez deux dés à la fois, votre chance d’obtenir deux six est : (probabilité d’un six sur le dé 1) x (probabilité d’un six sur le dé 2) = (1/6)⋅(1/6)=1/36.

En général, vous pouvez considérer la règle du produit comme la règle « ET » : si l’événement X et événement Y doivent avoir lieu pour qu’un certain résultat se produise, et si X et Y sont indépendants l’un de l’autre (n’affectant pas la probabilité l’un de l’autre), vous pouvez alors utiliser la règle du produit pour calculer la probabilité du résultat en multipliant les probabilités de X et Y.

EXEMPLE 1

Nous pouvons utiliser la règle du produit pour prédire les fréquences des événements de fécondation. Par exemple, nous pouvons envisager un croisement entre deux individus hétérozygotes (Aa). Quelles sont les chances d’obtenir un individu aa dans la prochaine génération ? La seule façon d’obtenir un individu aa est que la mère donne un gamète a et que le père donne également un gamète a. Chaque parent a 1/2 chance de produire un gamète a. Ainsi, la probabilité d’obtenir aa dans la progéniture est : (probabilité que la mère apporte a) x (probabilité que le père apporte a) = (1/2)⋅(1/2)=1/4.

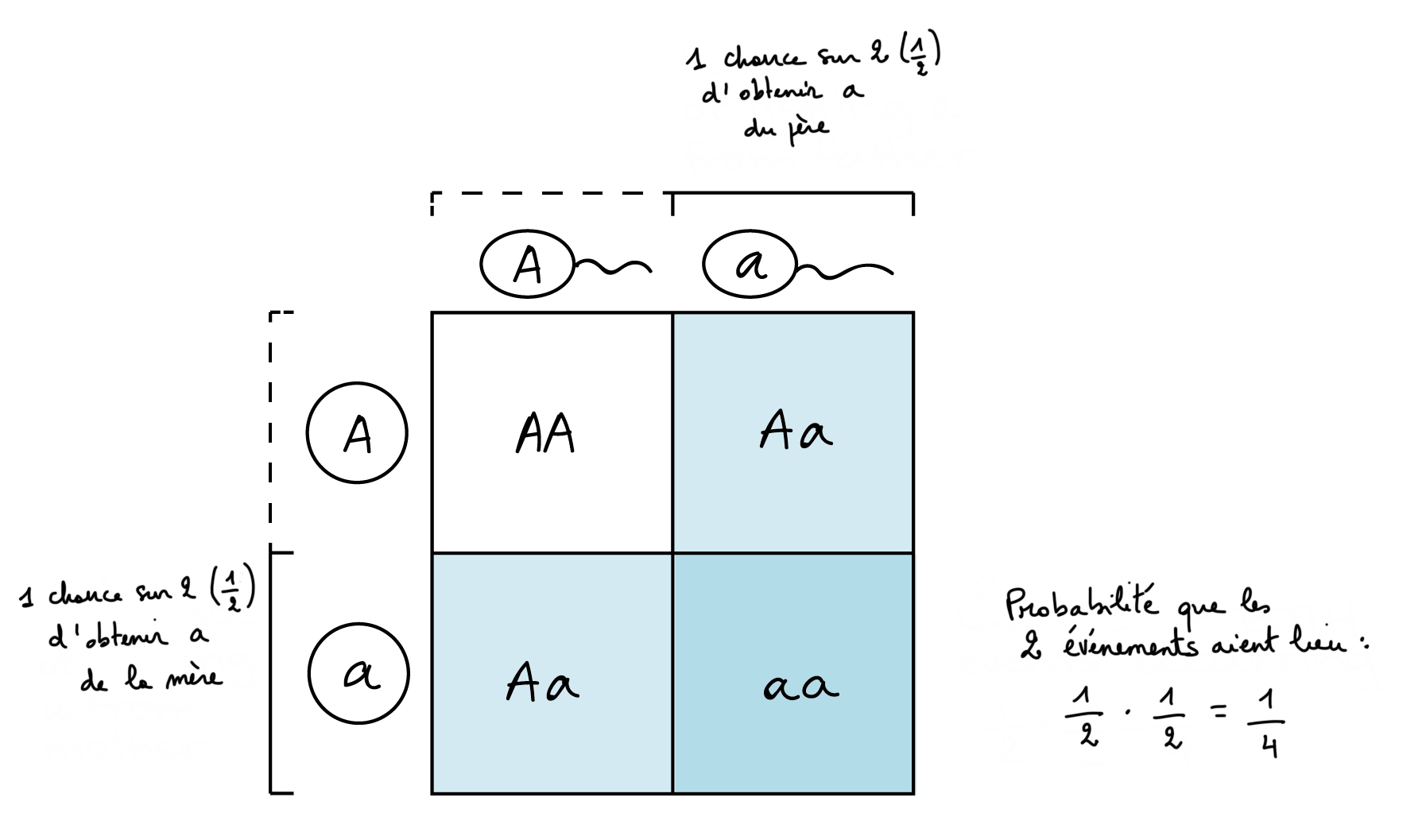
La règle de la somme en probabilité

Pour certains problèmes de génétique, vous aurez peut-être besoin de calculer la probabilité qu’un événement quelconque se produise. Dans ce cas, il faudra appliquer une autre règle de probabilité : la règle de la somme. Selon cette règle de la somme, la probabilité que n’importe quel événement parmi plusieurs événements mutuellement exclusifs se produise est égale à la somme des probabilités individuelles de ces événements.

Par exemple, si vous lancez un dé à six faces, vous avez une chance de 1/6 d’obtenir un nombre donné, mais vous ne pouvez obtenir qu’un seul numéro par lancer. On ne pourrait jamais obtenir à la fois un 1 et un 6 en même temps ; ces résultats sont mutuellement exclusifs. Ainsi, les chances d’obtenir un 1 ou un 6 sont : (probabilité d’obtenir un 1) + (probabilité d’obtenir un 6) = (1/6)+(1/6)=1/3.

Vous pouvez considérer la règle de la somme comme la règle « ou » : si un résultat nécessite que l’événement X ou l’événement Y se produise, et si X et Y sont mutuellement exclusifs (si un seul des deux événements peut se produire dans un cas donné), alors la probabilité du résultat peut être calculée en additionnant les probabilités de X et Y.

EXEMPLE 2

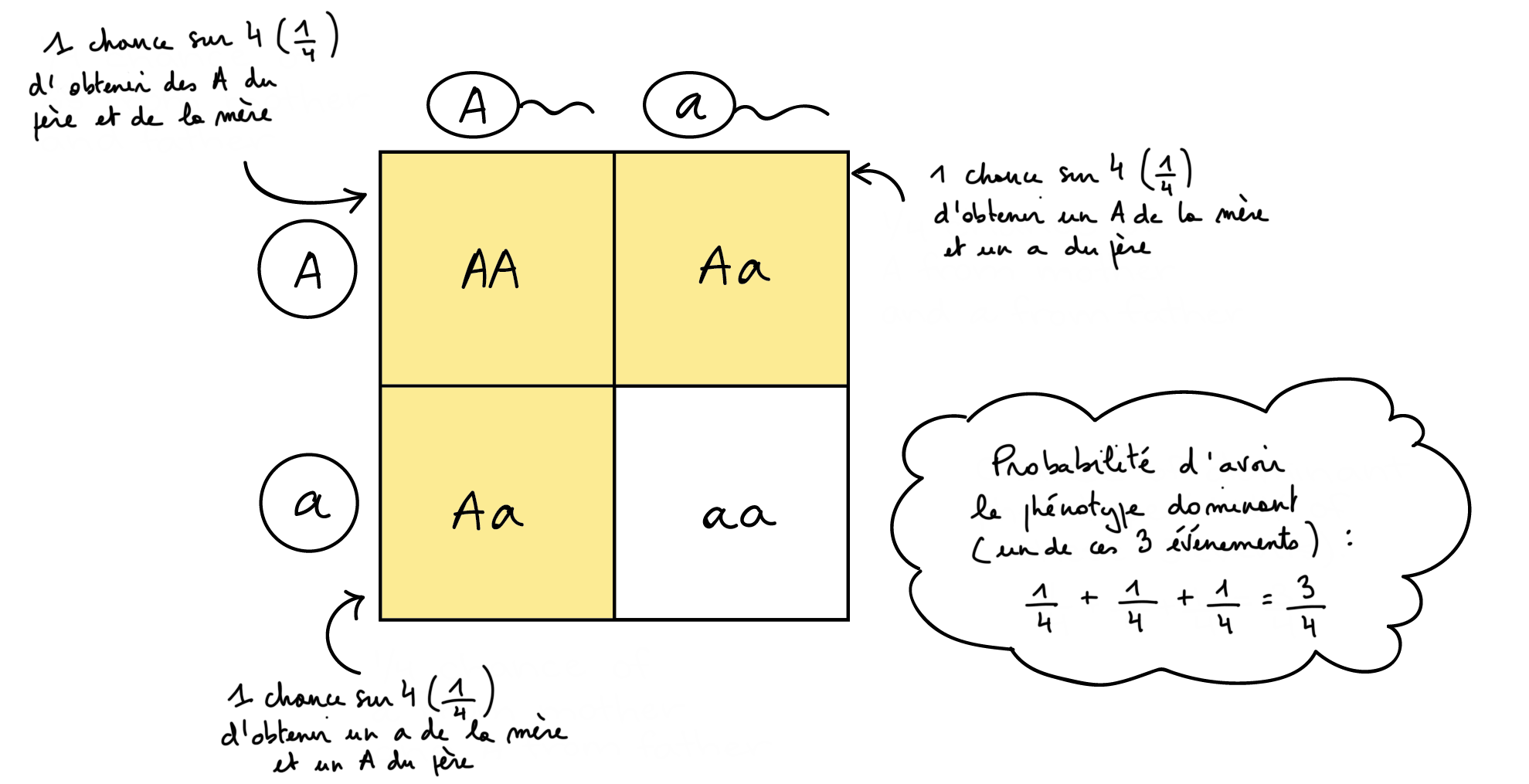
À titre d’exemple, utilisons la règle de la somme pour prédire la proportion de la progéniture d’un croisement Aa x Aa qui aura le phénotype dominant (AA ou Aa génotype). Dans ce croisement, il y a trois événements qui peuvent conduire à un phénotype dominant :

• Deux gamètes A s’assemblent (donnant un génotype AA), ou
• le gamète A de la mère s’assemble au gamète a du père (donnant un génotype Aa), ou
• le gamète a de la mère s’assemble au gamète A du père (donnant un génotype Aa)

Dans un événement de fécondation, une seule de ces trois possibilités peut se produire (elles sont mutuellement exclusives).

Puisqu’il s’agit d’une situation « ou » où les événements sont mutuellement exclusifs, nous pouvons appliquer la règle de la somme. En utilisant la règle de produit que nous avons appliquée ci-dessus, nous pouvons constater que chaque événement a une probabilité de 1/4. Ainsi, la probabilité que la progéniture ait un phénotype dominant est : (probabilité de A de la mère et A du père) + (probabilité de A de la mère et a de du père ) + (probabilité de a de la mère et A du père) = (1/4)+(1/4)+(1/4)=3/4.

CONCLUSION