Mathématiques
Ligne d’horizon et points de fuite en dessin d’art
La vision
La vision de nos trois traits au sol peut changer, comme tout élément de la scène.
Voici les paramètres qui peuvent changer la perspective d’un objet : la hauteur de notre œil par rapport au sol (=horizon =ligne de vision)
Le point de vue : là où nous nous tenons lorsqu’on observe un objet
Les points de fuite : points vers lesquels deux lignes parallèles semblent converger vers l’horizon.
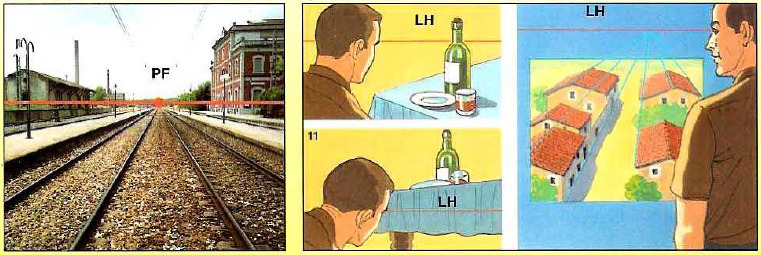
Un bon exemple pour illustrer ce phénomène : si vous êtes sur la plage et que vous regardez au loin, vous vous apercevrez que plus vous regardez loin, et plus les détails des vagues sembleront petits.
D’ailleurs on ne voit presque plus aucun détail aux alentours de l’horizon. Sans ce phénomène de perspective, nous verrions aussi
bien de près que de loin et toutes les vagues seraient de la même taille.

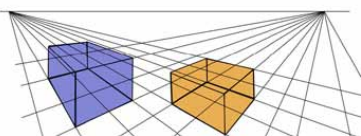
Une perspective ne s’applique pas à une scène entière, mais à un seul objet d’une même scène. Ce qui signifie que pour une même scène visuelle, et pour une même ligne de vision, on pourra représenter des objets à un, deux ou trois points de fuite, sans que ces points de fuite soient les mêmes pour tous les objets.
Bien qu’il s’agisse du plus rapide de tous les cas de figure de la perspective, ce n’est pas aussi simple qu’on pourrait le croire. Le piège de la perspective à un point de fuite est qu’une bonne partie de l’objet est dissimulée derrière l’avant plan de ce dernier.
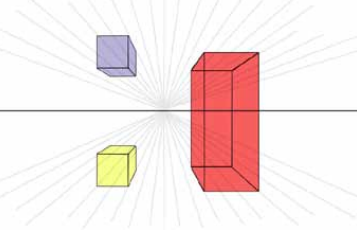
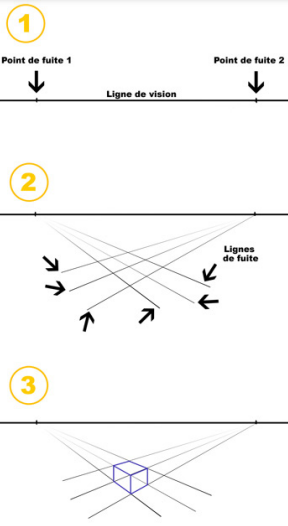
Bien qu’un peu plus lente à construire, la perspective à deux points de fuite révèle plus d’informations sur l’objet que la perspective à un point de fuite.
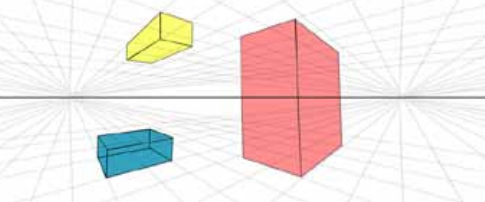
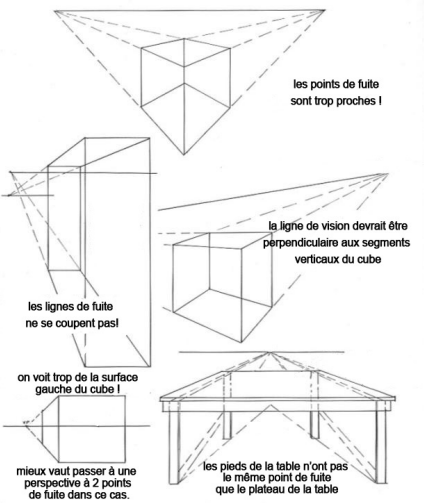
Les erreurs courantes dans la construction de la perspective
- Placer ses points de fuite trop près les uns des autres.
- Représenter un cube ou parallélépipède rectangle avec une discordance de point de fuite entre une face et une autre.
- Ne pas placer les points de fuite sur la même ligne de vision.
- Montrer trop d’une face d’un cube dans un dessin à deux points de fuite et faire comme s’il ne s’agissait que d’une perspective à un point de fuite.
- Représenter une table avec les pieds arrière trop bas. La perspective d’une table simple est aussi facile à représenter que celle d’un cube.
- Représenter un personnage ou un objet au premier plan qui n’est pas au bon niveau par rapport aux autres éléments de la scène.
- Projeter un motif aléatoirement.