Mathématiques
Evaluations statistiques + corrigés
EVALUATION MATHEMATIQUES Statistiques
2NDE Nature Jardin Paysage Forêt– 1ERE Aménagements Paysagers
Exercice 1
Les résultats seront arrondis à 10-1 près dans tout l’exercice.
Une étude porte sur la durée du trajet domicile-travail de 200 personnes.
Les résultats obtenus sont répertoriés dans le tableau ci-dessous.

La courbe des effectifs cumulés croissants est représentée sur le document 1.
- Calculer la moyenne
et l’écart type s de cette série statistique.
Aide méthodologique :
calculer le centre des classes,
5 ;15 ;25 ;35 ;45 ;55
utiliser votre calculatrice mode STAT
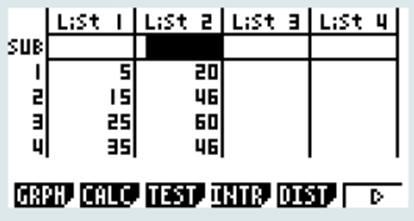
CALC + SET
exploiter les résultats de la calculatrice
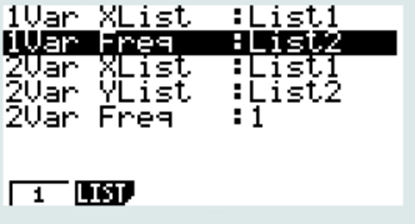
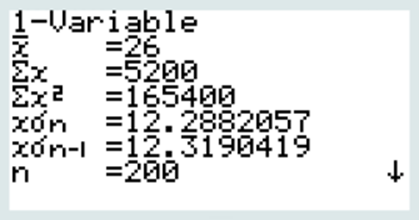
1 VAR
moyenne = 26……………………………………………………
écart-type = 12,29……………………………………………………
Vérification n=200 en effet : 20+46+60+46+24+4 = 200
- Pour chacune des affirmations suivantes, indiquer si elles sont vraies ou fausses, en justifiant la réponse.
Aide méthodologique :
Exploitation des résultats de la calculatrice OU lecture du document 1,
· La médiane de la série est égale à 100
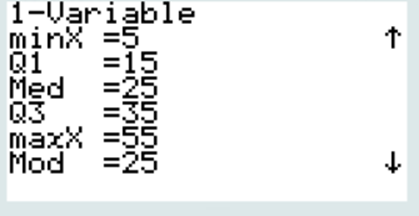
faux, la médiane Med = 25 donne un effectif à 100
OU Lecture graphique
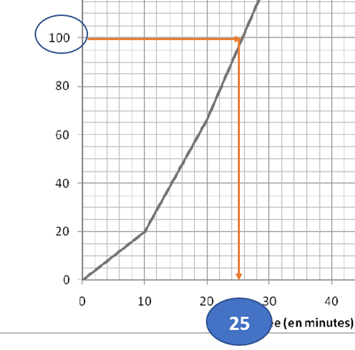
· Plus de la moitié des personnes interrogées ont un trajet domicile-travail supérieur à 25 minutes.
1 / 2 x 200 = 100
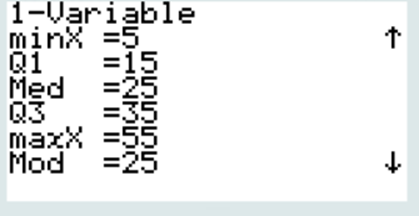
faux, la moitié est à 25 min de trajet (=Med)
· Environ 65 % des personnes interrogées ont un trajet domicile-travail d’une durée comprise entre 14 et 40 minutes.
65% x 200 = 130
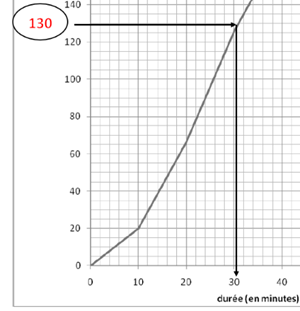
lecture graphique
durée du trajet 30 min, donc vrai.
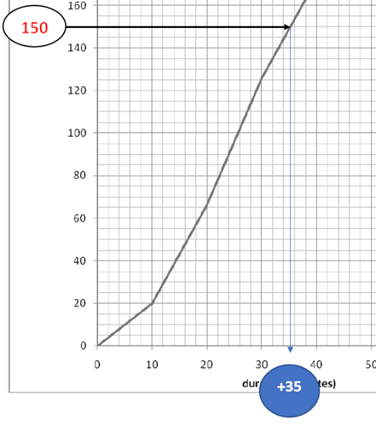
· des personnes interrogées ont un trajet domicile-travail d’une durée supérieure à 35 minutes.
3 / 4 x 200 = 150
Lecture graphique
vrai
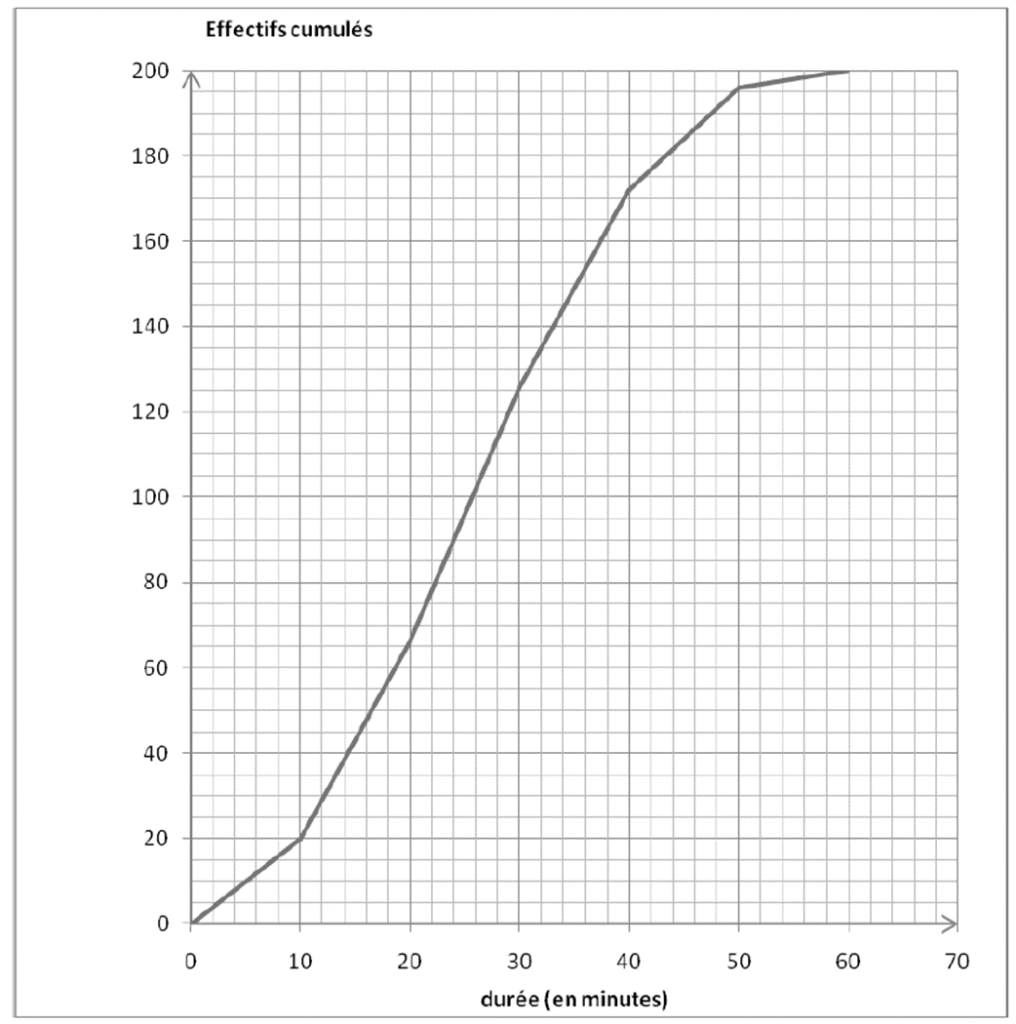
DOCUMENT 1
Courbe des effectifs cumulés croissants
Exercice 2
Une entreprise fabrique des fromages de chèvre sous forme de bûches.
A l’issue d’une journée de fabrication, elle mesure les masses de deux lots de 200 bûches chacun. Les résultats obtenus sont les suivants :
Lot A :

Lot B :
Masse moyenne de 250 g et écart-type s de 2,5 g.
- Calculer le pourcentage de bûches du lot A ayant une masse supérieure ou égale à 250 g.
centre des classes : 245 ;247 ;249 ;251 ;253 ;255
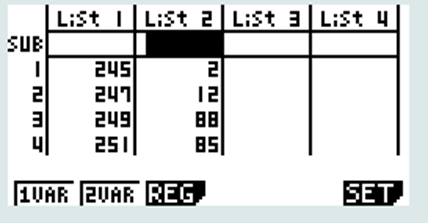
CALC + SET
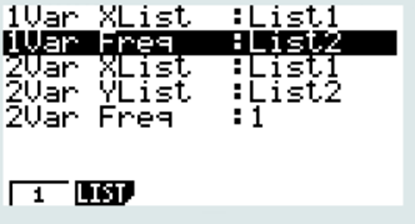
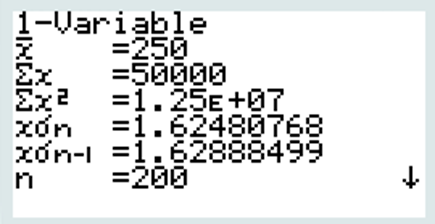
1 VAR
Nous retrouvons n=200 (en vérification)
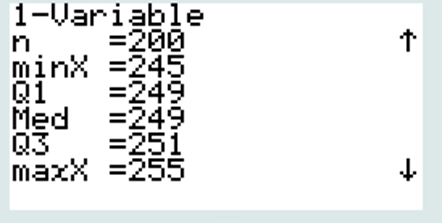
La calculatrice indique Q3 (3ème quartile) pour une masse de 251 g, soit 75%
Pour rappel Q1 = 25% ; Q2 = Med = 50% ; Q3=75%
- Les résultats suivants seront arrondis à 10-1 près.
- Déterminer la masse moyenne
des bûches du lot A.
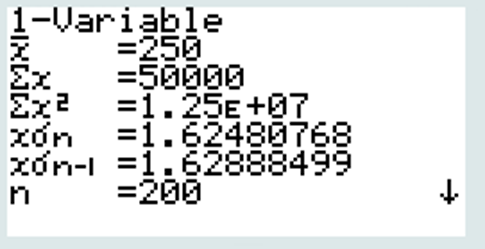
La moyenne est de 250,0 g
- Déterminer l’écart type s de la série de mesures du lot A.
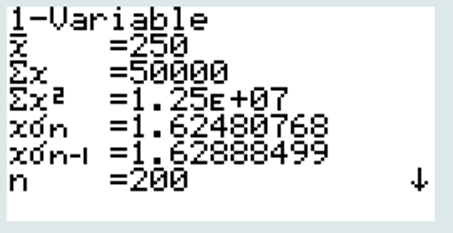
l’écart type s est de 1,6 g
- Comparer les paramètres de ces deux lots et conclure dans le cadre de cet exercice.
Les deux lots A et B ont la même moyenne à 250g. Toutefois le lot A est plus homogène que le lot B car son écart-type est plus petit que celui du lot B (A : s = 1,6 contre B : s = 2,5)
Exercice 3
Un groupement de producteurs souhaite proposer en vente directe des caissettes de viande de cabri issues de l’agriculture biologique. Pour cela, il doit rechercher d’autres producteurs afin de consolider les approvisionnements du groupement.
Maria, jeune agricultrice, rejoint le groupe de producteurs et fournit vingt colis, dont la masse en kg est donnée dans le tableau ci-dessous :
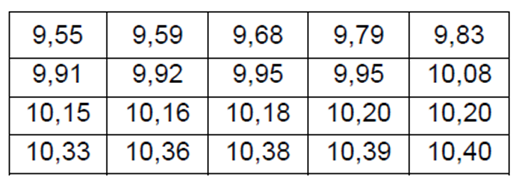
Dans cet exercice, le détail des calculs n’est pas demandé et ils pourront être effectués à l’aide de la calculatrice.
- Calculer l’étendue de cette série statistique.
Etendue e = 10,40 – 9,55 soit e =0,85 Kg

- Calculer la masse moyenne des caissettes. Donner le résultat arrondi à 10-2 près.
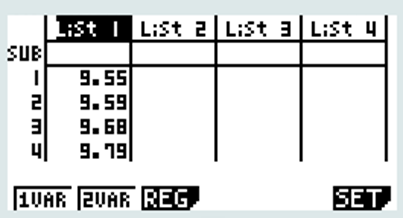
CALC + SET
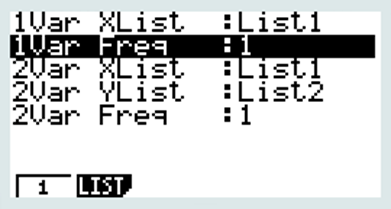
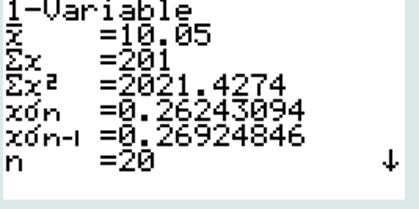
La moyenne est de 10,05 Kg
- Déterminer la masse médiane des caissettes.
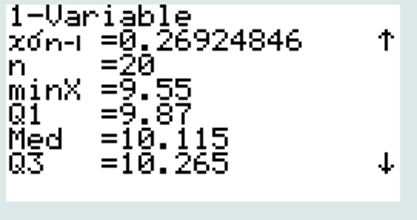
La médiane Med = 10,12 Kg
- Déterminer l’écart-type. Donner le résultat à 10-2 près.
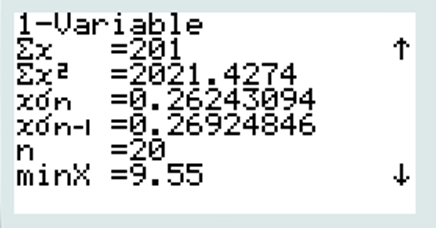
l’écart type s est de 0,26 Kg
Jean, un deuxième éleveur, propose également 20 caissettes, dont les paramètres statistiques sont les suivants :
Étendue = 1,20 kg ; moyenne = 9,95 kg ; médiane = 10,05 kg et écart-type = 0,52 kg.
Jean affirme que ses caissettes sont en moyenne plus lourdes et plus homogènes que celles de Maria.
Jean a-t-il raison ? Justifier votre réponse.
« Les caissettes de Jean sont en moyenne plus lourdes que les caissettes de Maria. » Cette affirmation est fausse car la moyenne = 9,95 kg (Jean) contre La moyenne
est de 10,05 Kg (Maria)
« Les caissettes de Jean sont plus homogènes que les caissettes de Maria. » Cette affirmation est fausse car l’écart-type = 0,52 kg (Jean) contre l’écart-type = 0,26 kg. (Maria). De plus l’étendue e = 1,20 kg (Jean) est plus importante que l’étendue e = 0,85 kg (Maria)
