Introduction

Carl Friedrich Gauss conçoit une loi statistique continue, appelée loi normale ou loi de Laplace-Gauss, dont la répartition est représentée par la fameuse courbe en cloche.
L’adjectif « normale » s’explique par le fait que cette loi décrit et modélise des situations statistiques aléatoires concrètes et naturelles

Exemple 1 : Situation suivant une loi normale

Un site de vente en ligne de vêtements établit le bilan des ventes par taille. L’histogramme ci-dessous résume ce bilan.

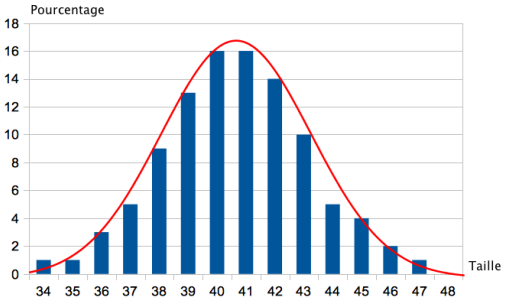
On désigne par X la variable aléatoire qui donne la taille souhaitée par un client connecté. X prend des valeurs entières dans l’ensemble {34 ; 35 ; 36 ; … ; 47 ; 48}.

On recherche la probabilité p pour une situation donnée. Par exemple, quelles sont les probabilités d’obtenir une taille de vêtement en 40, 45 ou comprise entre 37 et 40 ?
On écrit la relation : P(X = 40) = 16% (lecture du résultat sur l’histogramme)

On écrit la relation : P(X = 45) = 4% (lecture du résultat sur l’histogramme)

On écrit la relation : P(37 ≤ X ≤ 40) = 5 + 9 + 13 + 16 = 43% (lectures des résultats sur l’histogramme)

On a tracé la courbe d’une fonction f qui s’approche de l’histogramme. Dans ce cas, on considère la variable aléatoire Y qui donne la taille souhaitée par le client connecté. Y prend des valeurs réelles dans l’intervalle [34 ; 48].

La probabilité P(37 ≤ Y ≤ 40) correspond à l’aire sous la courbe de la fonction f entre les droites d’équation x = 37 et x = 40 .

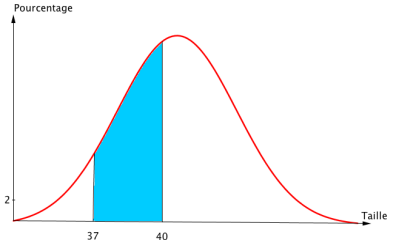
Description d’une situation suivant une loi normale

La courbe représentative de la fonction associée à la loi normale est une courbe en cloche symétrique par rapport à la droite d’équation x = µ .

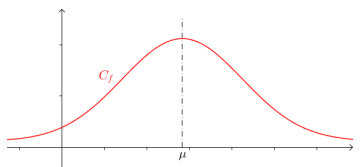
Espérance et écart-type d’une loi normale

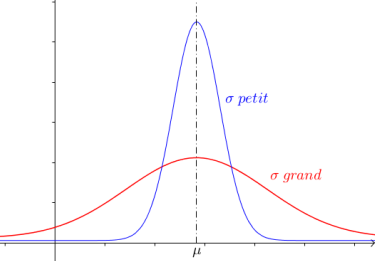
• L’espérance, notée µ , donne la valeur moyenne.
• L’écart-type, noté σ , donne la dispersion autour de la moyenne.

La courbe est d’autant plus « resserrée » autour de son axe de symétrie que l’écart-type σ est petit.

TD : Calcul de la Probabilité sur une loi normale (utilisation calculatrice CASIO)

Une compagnie de transport possède un parc de 200 cars. On appelle X, la variable aléatoire qui, à un car choisi au hasard associe la distance journalière parcourue. On suppose que X suit la loi normale d’espérance µ = 80 et d’écart-type σ = 14 .
Quelle est la probabilité, à 10^-3 près, qu’un car parcourt :
1) Entre 70 et 100 km par jour ?
2) Moins de 90 km par jour ?
3) Plus de 100 km par jour ?

ELEMENTS DE REPONSE

1- Calcul de la probabilité que le cars parcours entre 70 et 100 km par jour.

Taper sur la touche [OPTN], puis dans l’ordre [STAT], [DIST], [NORM] et [Ncd] puis saisir NormCD(70,100,14,80)

La fonction utilisée est Ncd pour Normal Cumulative Distribution

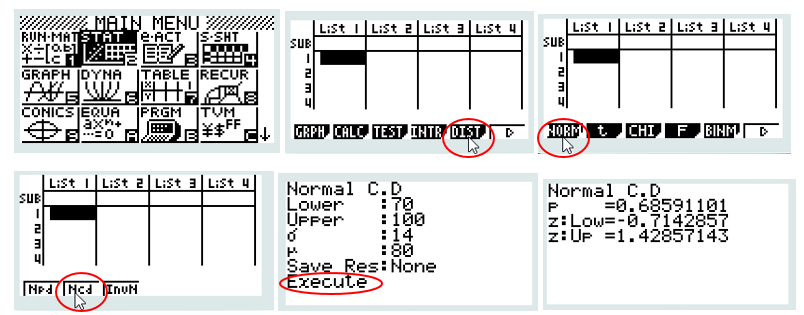
CONCLURE : On a ainsi : P(70 ≤ X ≤ 100) ≈ 0,686 . La probabilité qu’un car parcourt entre 70 et 100 km par jour est d’environ p=0,686 ou encore p=68,6%.

2- Calcul de la probabilité que le cars parcours moins de 90 km par jour

Taper sur la touche [OPTN], puis dans l’ordre [STAT], [DIST], [NORM] et [Ncd] puis saisir NormCD(0,90,14,80)

La fonction utilisée est Ncd pour Normal Cumulative Distribution

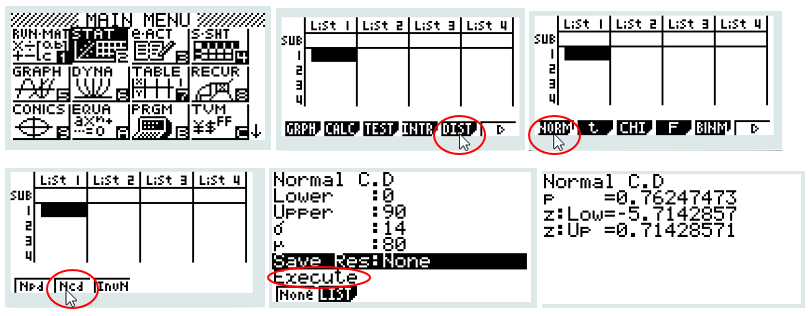
CONCLURE :

On a ainsi : P( X ≤ 90) ≈ 0,762 . La probabilité qu’un car parcourt moins de 90 km par jour est d’environ p=0,762 ou encore p=76,2%.

3- Calcul de la probabilité que le cars parcours plus de 100 km par jour

Taper sur la touche [OPTN], puis dans l’ordre [STAT], [DIST], [NORM] et [Ncd] puis saisir NormCD(100,10^99,14,80)

La fonction utilisée est Ncd pour Normal Cumulative Distribution

10^99, nombre extrêmement grand, pour indiquer l’infini.

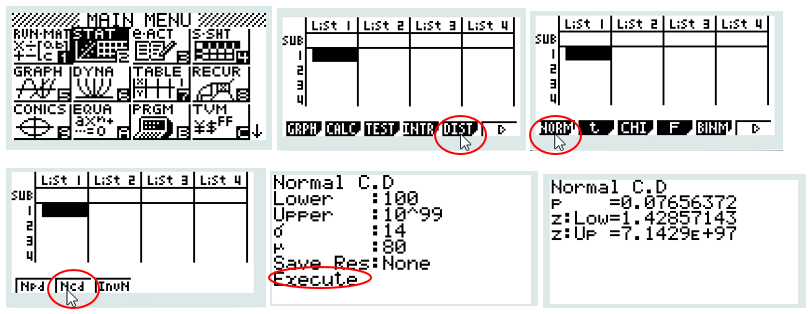
CONCLURE : On a ainsi : P( X ≥100) ≈ 0,077 . La probabilité qu’un car parcourt plus de 100 km par jour est d’environ p=0,077 ou encore p=7,7%.

Programmation calculatrice CASIO

Télécharger le fichier ProbaLoiNormale sur votre PC. Connecter votre calculatrice CASIO avec un cable USB, choisir mode de connexion « clé USB » en appuyant sur [F1]. Décharger votre fichier « ProbaLoiNormale.g1m » dans votre calculatrice / répertoire « @MainMem » / « PROGRAM« 

Exemple 2 : Situation suivant une loi normale

Une variable aléatoire X suit une loi normale d’espérance µ=20 et d’écart-type σ=3. Donner un intervalle de centre 20 qui contient environ 95% des valeurs prises par X.

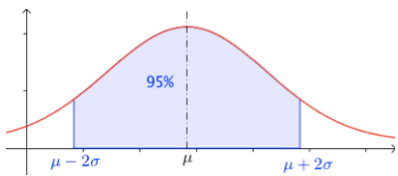
P(µ − 2σ ≤ X ≤ µ + 2σ ) = 0,95

Soit : P(20-2×3 ≤ X ≤ 20+2×3) = 0,95

Donc, P(14 ≤ X ≤ 26)=0,95