Définition

• On appelle épreuve de Bernoulli toute épreuve à deux issues possibles : un succès (noté S) ou un échec (noté S barré).
• La loi de Bernoulli est la loi de probabilité de la variable aléatoire Y prenant la valeur 1 si l’issue est un succès, et 0 si l’issue est un échec. On note p = p(Y = 1) = p(S). p est appelé paramètre de la loi de Bernoulli.

Schéma de Bernoulli – Loi binomiale

On appelle schéma de Bernoulli d’ordre n l’expérience consistant à répéter n fois de manière indépendantes la même épreuve de Bernoulli de paramètre p.
• La loi binomiale de paramètres n et p est la loi de probabilité de la variable aléatoire X prenant prenant comme valeurs le nombre de succès (S) obtenus au cours des n épreuves du schéma de Bernoulli.
• On dit aussi que loi loi de probabilité de la variable aléatoire X suit la loi binomiale de paramètres n et p.

Le nombre de chemins de l’arbre pondéré associé à un schéma de Bernoulli d’ordre n conduisant à k succès pour n répétitions est noté :

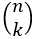
Ces nombres entiers se lisent « k parmi n » et sont appelés coefficients binomiaux.

Soit X une variable aléatoire suivant la loi binomiale de paramètres n et p

Les valeurs de X sont {0 ; 1 ; 2 ; . . . ; n} et Pour tout k ∈ {0 ; 1 ; 2 ; . . . ; n} :

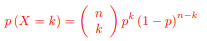
une situation relève de la loi binomiale dès lors que l’on :

• considère une expérience aléatoire (lancer d’une pièce, d’un dé, …)
• décide qu’un événement que l’on choisit sera appelé « Succès » (pile, 6, …)
• connaît la probabilité p de l’événement « Succès » (p = 0, 5 ; p = 1/6 ; …)
• répète cette expérience un certain nombre de fois avec indépendance (n = 10 par exemple)
• s’intéresse au nombre X de fois que l’on a obtenu un « Succès » parmi les n expériences. X = 0 : aucun succès ; … ; X=10 : 10 succès
• cherche à obtenir la valeur de la probabilité d’un événement concernant X (p(X = 0) =? par exemple)

Espérence, variance, écart-type

Soit X une variable aléatoire suivant la loi binomiale de paramètres n et p.

• Son espérance ( valeur que l’on s’attend à trouver, en moyenne) est : E (X) = np

• Sa variance (mesure de la dispersion des valeurs d’un échantillon) est : V (X) = np (1 − p)

• Son écart-type (sert à mesurer la dispersion, ou l’étalement, d’un ensemble de valeurs autour de leur moyenne) est : σ (X) = √ (np^{(1 − p)}) . Plus l’écart-type est faible, plus la population est homogène.

Exercice 1 : Lancé d’une pièce (résolution avec calculatrice CASIO)

On lance 20 fois de suite une pièce équilibrée. X est la variable aléatoire qui indique le nombre de sorties de « Face ».
On sait que X suit la loi binomiale de paramètres n=20 et p=0, 5.

1- Déterminer les coefficients binomiaux

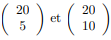
2- Calculer, à 10⁻⁴ près, p (X = 5) et p (X ≤ 10)

ELEMENTS DE REPONSE

1- Déterminer les coefficients binomiaux

Dans le menu [RUN], appuyer sur la touche [OPTN], puis choisir [PROB]

Taper 20, puis choisir nCr, puis taper 5 et [EXE].

Taper 20, puis choisir nCr, puis taper 10 et [EXE].

2a- Calculer, à 10⁻⁴ près, p (X = 5)

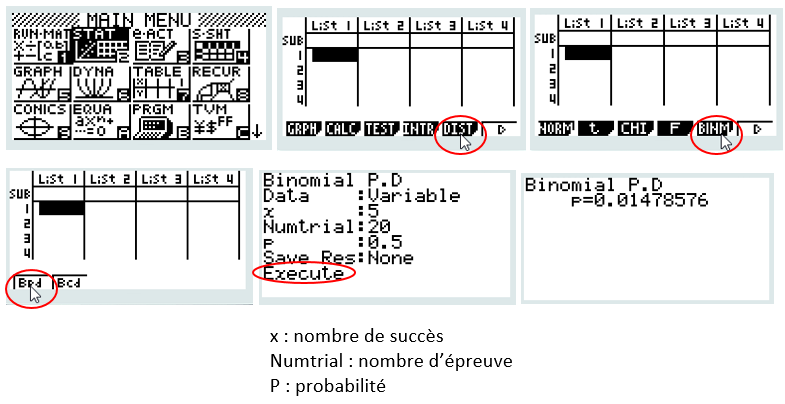
CONCLURE : La probabilité d’obtenir 5 succès pour 20 essais est p (X = 5) = 0,0148

2b- Calculer, à 10⁻⁴ près, p (X ≤ 10)

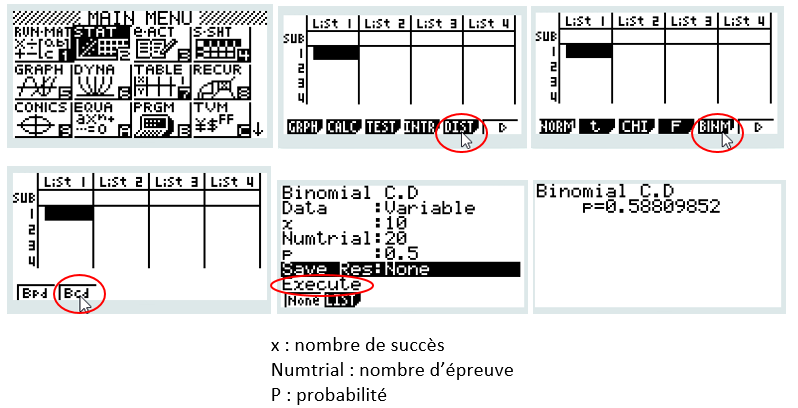
CONCLURE : La probabilité d’obtenir au plus 10 succès pour 20 essais est p (X ≤ 10) = 0,5881

Exercice 2 : Intérogations en classe (résolution avec calculatrice CASIO)

Soit une classe compte 30 élèves dont 20 filles. A chaque cours de mathématiques, le formateur interroge au hasard un élève de la classe, sans se rappeler quels élèves il a déjà interrogés.
On considère un entier positif ou nul n et on note X la variable aléatoire qui correspond au nombre de filles interrogées au cours de jours consécutifs.

1) Quelle est la loi de X ?
2) Quelle est la probabilité que sur 10 jours consécutifs, soient interrogées 4 filles exactement ? au moins 4 filles ?
3) Quel doit être le nombre minimal de cours consécutifs pour que la probabilité qu’aucune fille ne soit interrogée soit inférieure à 0,001 ?

ELEMENTS DE REPONSE

1- Nature de la loi suivie par la variable aléatoire X

Les interrogations se font de manière indépendante les unes des autres et à chaque interrogation la probabilité d’avoir une fille est 20/30 soit 2/3 donc, X suit une loi binomiale de paramètres n et p= 2/3 soit B(n , 2/3)

2a- Calculer à 10^-3 près, P(X=4) avec n=10 et p=2/3

Appliquer la relation ci-dessous

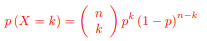
Programmation calculatrice CASIO

Télécharger le fichier CAL PROB sur votre PC. Connecter votre calculatrice CASIO avec un cable USB, choisir mode de connexion “clé USB” en appuyant sur [F1]. Décharger votre fichier “CAL PROB.g1m” dans votre calculatrice / répertoire “@MainMem” / “PROGRAM“

le programme ci-dessus vous permet d’automatiser le calcul

pour n=10 ; p=2/3 et k=4, nous obtenons P(X=4)= 0,0569 soit P(X=4)= 0,057 à 10^-3 près.

2b- Calculer P(X≥4) avec n=10 et p=2/3

Utiliser le même programme avec k=3 pour calculer P(X ≥ 4)= 1 − P(X ≤ 3) soit 1-0,016 soit P(X≥4) =0,984 à 10^-3 près.

3- Déterminer n pour P(X=0) ≤ 0,001 , avec p=2/3 et k=0 pour une probabilité qu’aucune fille ne soit interrogée soit inférieure à 0,001.

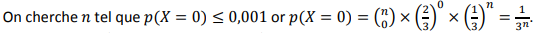
soit P(X=0) ≤ 0,001 soit 3ⁿ ≥ 1000 (attention au changement de signe)

Or, pour tout entier relatif n, d’après les proriétés de la fonction logarithme népérien (ln), nous savons que si x est un réel strictement positif alors  n . ln(x) = ln(xⁿ).

D’où, ln(3ⁿ) ≥ ln1000 soit n ln 3 ≥ ln1000 soit n ≥ ln1000/ln 3 soit n ≥ ln(1000/3)

ln(1000/3) ≥ 5,809 à 10^-3 près. donc, n ≥ 6 (nombre entier naturel)

Il faut donc interroger pendant au moins 6 jours consécutifs pour que la probabilité de n’avoir aucune fille soit inférieure à 0,001.