Introduction

On définit un échantillon de taille n par la répétition de n épreuves indépendantes d’une même expérience aléatoire à deux issues notées 0 et 1 (épreuve dite de Bernoulli).
La fluctuation d’échantillonnage (phénomène naturel fréquent) invite à se poser la question de la confiance envers les résultats trouvés.

Il est admis : « pour des échantillons de taille n ≥ 25 et de proportion p du caractère comprise entre 0,2 et 0,8 : si f désigne la fréquence du caractère dans l’échantillon, f appartient à l’intervalle avec une probabilité d’au moins 0,95. 

Cet intervalle est nommé intervalle de fluctuation au seuil de 95 %».

Exercice 1 : Election présidentielle et intervalle de fluctuation

Entre les deux tours d’une élection présidentielle, il ne reste que deux candidats A et B en lice. Lors d’un débat télévisé, A affirme sur la foi d’un sondage secret que si l’élection avait lieu maintenant, il gagnerait largement avec 60% des voix. Avant la fin du débat, B fait effectuer un sondage par téléphone auprès de 200 personnes en âge de voter. Le résultat donne 104 personnes en faveur de A.
1) En supposant que le sondage secret reflète fidèlement l’opinion des électeurs le jour du débat, donner l’intervalle de fluctuation à 95% de la fréquence des personnes favorables à A sur un échantillon de 200 pesonnes.
2) Que peut-on dire suite au résultat du sondage demandé par B ?
3) Reprendre les deux questions avec un intervalle de fluctuation au seuil de 98%.

ELEMENTS DE REPONSE

1- Intervalle de fluctuation à 95%

Selon le candidat A, 60% voteraient pour lui, soit p=60% ou encore p=0,6. Le sondage porte sur n=200 personnes. Appliquer la relation ci-dessous pour déterminer l’intervalle de fluctuation I_n.

Déterminons la valeur de u_⍺ avec la calculatrice CASIO pour appliquer la formule de l’intervalle de fluctuation au seuil de 1-⍺ (cas général)

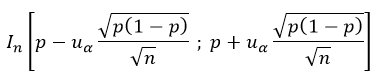
Pour un seuil à 95%, nous avons 1-⍺ = 0,95 d’où ⍺ = 0,05

Au seuil de 95% : (1-0,95)/2 = 0,025 donc on cherche a et b tels que P(X ≤ a) > 0,025 et P(X≤ b) ≥ 0,975 pour déterminer l’intervalle de fluctuation I = [a/n ; b/n]

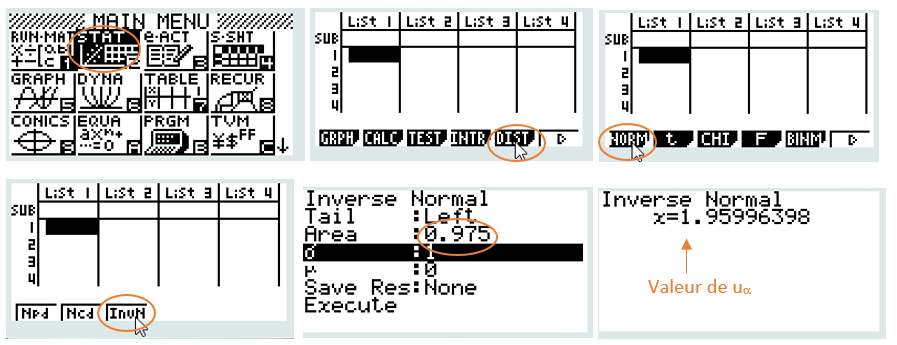
Appliquons la valeur de u_⍺ dans la formule de l’intervalle de fluctuation avec la calculatrice CASIO, à 10^-2 près

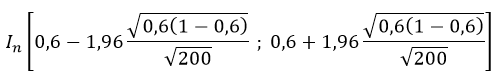
CONCLURE :

P(X ≤ 106) > 0,025 et P(X≤ 134)= 0,975

L’intervalle de fluctuation à 95% est donc I [0,53 ; 0,67]

2- Interprétation du résultat du sondage commandé par le candidat B

104 personnes par rapport aux 200 interrogées représentent une fréquence de f = 104/200 soit f= 0,52

CONCLURE : Cette fréquence f n’appartient pas à l’intervalle de fluctuation I [0,53 ; 0,67] donc on peut rejeter l’hypothèse que le candidat A dit vrai, avec un risque de 5% de rejeter cette hypothèse à tort.

3- Intervalle de fluctuation au seuil de 98%

Pour réduire le risque de rejeter à tort une hypothèse, nous pouvons passer d’un seuil de risque de 5% à un seuil de risque de 2%. Pour celà, il faut redéfinir l’intervalle de fluctuation non plus à 95%, mais à 98%.

Déterminons la valeur de u_⍺ avec la calculatrice CASIO pour appliquer la formule de l’intervalle de fluctuation au seuil de 1-⍺ (cas général)

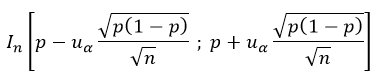
Pour un seuil à 98%, nous avons 1-⍺= 0,98 d’où ⍺=0,02

Au seuil de 98% : (1-0,98)/2 = 0,01 donc on cherche a et b tels que P(X ≤ a) > 0,01 et P(X≤ b) ≥ 0,99 pour déterminer l’intervalle de fluctuation I = [a/n ; b/n]

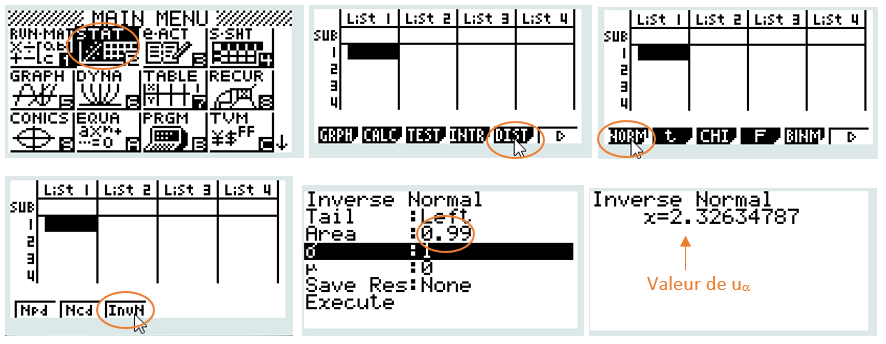
Appliquons la valeur de u_⍺ dans la formule de l’intervalle de fluctuation avec la calculatrice CASIO, à 10^-2 près

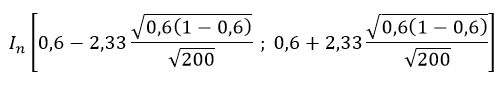
soit I [0,52 ; 0,68]. La valeur de a est 0,52 x 200 soit a = 104 et la valeur de b est 0,68 x 200 soit b = 136

CONCLURE :

P(X ≤ 104) > 0,01 et P(X≤ 136) ≥ 0,99

L’intervalle de fluctuation à 95% est donc I [0,52 ; 0,68]

104 personnes par rapport aux 200 interrogées représentent une fréquence de f = 104/200 soit f= 0,52

CONCLURE : Cette fréquence f appartient à l’intervalle de fluctuation I [0,52 ; 0,68] donc on peut accepter l’hypothèse que le candidat A dit vrai, avec un risque de 2% d’accepter cette hypothèse à tort.

Programmation calculatrice CASIO

Télécharger le fichier ALGO2 sur votre PC. Connecter votre calculatrice CASIO avec un cable USB, choisir mode de connexion “clé USB” en appuyant sur [F1]. Décharger votre fichier “ALGO2.g1m” dans votre calculatrice / répertoire “@MainMem” / “PROGRAM“

Pour résoudre automatiquement les questions, saisir les paramètres suivants. Les résultats sont plus précis car il n’y a pas d’arrondi dans les calculs intermédiaires.

N = 200 ; P = 0,6 ; Seuil de confiance = 0,975 ; résultats pour P(X ≤ a) > 0,025: a = 106 ; et P(X≤ b) ≥ 0,975 : b = 133

N = 200 ; P = 0,6 ; Seuil de confiance = 0,99 ; résultats P(X ≤ a) > 0,01: a = 104 ; et P(X≤ b) ≥ 0,99 ; b = 136