1.      Introduction

Soit la fonction f(x) = x² + x – 2 sur l’intervalle [-3 ; 2]. Remplir le tableau de valeurs suivant puis tracer la représentation graphique de f(x) sur cet intervalle.

Indiquer les valeurs de x pour lesquelles f(x) = 0.

Pour x = -2 et x = 1.

L’équation du second degré –x² + x – 2 = 0 a donc 2 solutions.

x₁ = -2             x₂ = 1              S = {-2 ;1}

On appelle discriminant du trinôme ax ² + bx + c , le nombre réel, noté Δ, égal à b² − 4ac

Application avec a=1 ; b=1 ; c=-2

Δ =1² – 4.1.(-2) = 9, d’où racine carrée de Δ = 3

d’où x₁=(-1-3) / (2 . 1), d’où x₁ = -2

et x₂ = (-1+3) / (2 . 1), d’où x₂ = 1

2.      La dérivation d’une fonction de second degré.

le principe pour passer d’une fonction de second degré à une fonction de premier degré est la suivante :

2nd degré : y = a.x² + b.x + c peut également s’écrire y=a.x² + b.x¹ + c.x⁰

rappels : un nombre à la puissance 1 est lui même, c’est-à-dire x¹ = x

rappel : un nombre à la puissance 0 est toujours égal à 1, c’est-à-dire x⁰ = 1

Pour passer au 1er degré, il suffit de multiplier le terme par l’exposant comme ci-dessous, puis de baisser un cran l’exposant

y’= 2.a.x ^(2-1) + 1.b.x^(1-1) + 0.c.x^(0-1)

ce qui donne, y’=2.a.x¹ + b.x⁰ + 0

soit y’=2.a.x + b, c’est une fonction affine

Sachant cela, vous pouvez directement appliquer la dernière relation (y’=2ax+b) pour dériver une fonction de second degré (y=ax²+bx+c).

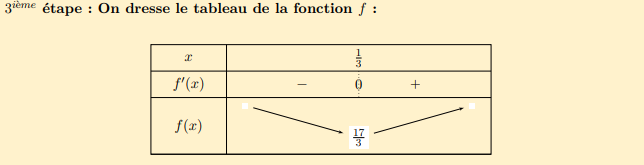
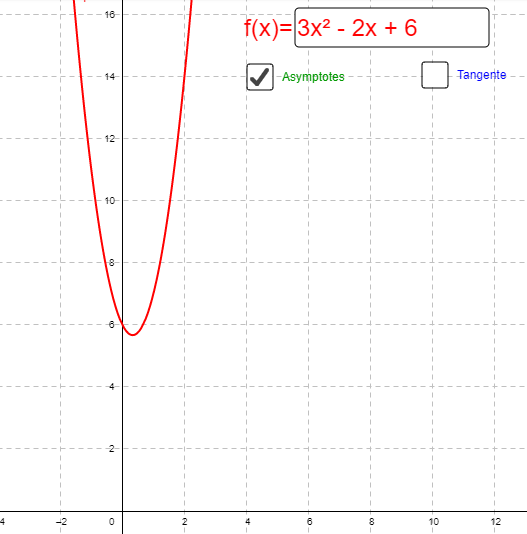
Soit la fonction f(x) = 3x² – 2x +6 sur l’intervalle [-2 ; 3].

A l’aide du logiciel Géogébra, tracer la fonction : https://www.geogebra.org/m/gBH4Dya4

Exercice

Soit la fonction f(x)=-5x²+10x+15 sur l’intervalle [-1 ; 3]. Déterminer sa fonction dérivée f ‘ (x)

1. Dérivation

y’= 2.(-5).x + 10, soit y’ = -10x+10

2.Tableau de variation

Calculer aux bornes f(-1) et f(3). Résultats attendus f(-1)=0 et f(3)=0

Calculer l’extremum f(-b/(2a)) = f(1). Résultat attendu f(1)=20

Dresser le tableau de variation

3. Déterminer les solution de l’équation de second degré